Типовые задания школьного этапа Всероссийской олимпиады школьников Пятый класс
5.1. На уроке физкультуры мальчики построились в шеренгу. Потом между каждыми двумя мальчиками встала девочка. Всего в шеренге оказалось 25 детей. Сколько мальчиков стояло в шеренге?
Ответ. 13. Решение. Уберем самого правого мальчика. Тогда мальчиков и девочек будет поровну, то есть по 12. Значит, в шеренге стояло 12 + 1 = 13 мальчиков.
5.2. Замените буквы A, B, C, D цифрами так, чтобы получилось верное равенство АААА + ВВВ + CC + D = 2014.
Ответ. 1111 + 888 + 11 + 4 = 2014.
5.3. Составьте из шести прямоугольников 7x1, 6x1, 5x1, 4x1, 3x1, 2x1 и квадрата 1x1 прямоугольник, у которого каждая сторона больше 1.
Решение. Из прямоугольника 6x1 и квадрат 1x1 сложим прямоугольник 7x1. Аналогично сложим прямоугольники 7x1 из пар прямоугольников 5x1, 2x1 и 4x1, 3x1. Из четырех полученных прямоугольников 7x1 складывается прямоугольник 7x4.
5.4. В 9.00 Юра вышел из дома и пошёл по прямой дороге со скоростью 6 км/ч. Через некоторое время он развернулся и с той же скоростью пошёл домой. В 12.00 Юре оставалось до дома два километра. На каком расстоянии от дома он развернулся? Объясните, как был найден ответ.
Ответ. На расстоянии 10 км. Решение. За 3 часа, с 9.00 до 12.00, Юра прошёл 18 км. Если он пройдет еще два километра, то он попадет домой. То есть 18 + 2 = 20 км. – это путь до места разворота и обратно. Значит, он развернулся на расстоянии 20:2 = 10 км от дома. 5.5. Кот Матроскин прикинул, что он может выложить пол квадратной комнаты квадратной плиткой, и ему не понадобится ни одну из них разрезать. Сначала он положил плитки по краям комнаты, и на это у него ушло 84 плитки. Сколько всего ему надо иметь плиток, чтобы покрыть весь пол?Ответ. 484.
Решение. На каёмке, не считая угловых, лежит 84 – 4 = 80 плиток. Значит, на каждой
стороне лежит 20 плиток, не считая угловых, а вместе с угловыми – 22 плитки. Поэтому
общее число плиток равно 484.
Шестой класс
Решение школьного тура олимпиады 6 класс
6.1. Как разложить гирьки весом 1, 2, ..., 9 г в три коробочки так, чтобы в первой было две гирьки, во второй – три, в третьей – четыре, а суммарный вес гирек в коробочках был
одинаковым?
Ответ. Например: 9 + 6; 8 + 5 + 2; 7 + 4 + 3 + 1.
Решение. Суммарный вес гирек равен 45, поэтому в каждой коробочке суммарный вес гирек равняется 15 г.
6.2. Мальчик по чётным числам всегда говорит правду, а по нечётным всегда врёт. Как-то его три ноябрьских дня подряд спрашивали: «Как тебя зовут?». На первый день он
ответил: «Андрей», на второй: «Борис», на третий: «Виктор». Как зовут мальчика? Объясните, как вы рассуждали.
Ответ. Борис.
Решение. Так как мальчик дал три разных ответа, он хотя бы два раза соврал. Поэтому два дня из трёх, когда мальчику задавали вопросы, пришлись на нечётные числа. Поскольку
чётные и нечётные числа месяца чередуются, это должны были быть первый и третий дни. Стало быть, второй день пришёлся на чётное число. В этот день мальчик и назвал своё
настоящее имя.
6.3. Мышь, мышонок и сыр вместе весят 180г. Мышь весит на 100г больше, чем мышонок и сыр вместе взятые. Сыр весит в три раза меньше, чем мышонок. Сколько весит
каждый из них? Ответ нужно подтвердить вычислениями.
Ответ. Мышь – 140г, сыр – 10г, мышонок – 30г.
Решение. Из условия следует, что удвоенный вес мыши равен 180 + 100 = 280г.
Поэтому вес мыши равен 140г. Тогда мышонок и сыр вместе весят 180 – 140 = 40г. А вес
сыра, согласно условию, равен четверти этого веса.
6.4. Как разрезать квадрат на семь треугольников, среди которых есть шесть одинаковых?
Решение. Два способа сделать это показаны на рис. 1. Есть и другие способы.
Рис. 1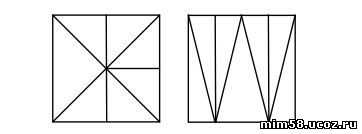
6.5. Есть 24 палочки. Длина первой палочки – 1 см, второй – 2 см, …, двадцать четвёртой – 24 см (длина каждой следующей палочки на 1 см больше длины предыдущей).
Как, использовав все эти палочки, составить три различных квадрата? Ломать палочки нельзя, каждая палочка должна входить только в один квадрат.
Решение. Разобьем палочки на три группы: от 1 до 8, от 9 до 16, от 17 до 24. В каждой группе первую палочку соединим с последней, вторую – с предпоследней, третью – с третьей
с конца, оставшиеся две палочки тоже соединим. Получим в каждой группе по четыре одинаковых палки, из которых сложим квадрат. Стороны полученных квадратов: 9, 25, 41.
Замечание. Есть и другие способы сложить три квадрата.
Седьмой класс
Решение школьного тура олимпиады 7 класс
7.1. К Васе пришли его одноклассники. Мама Васи спросила у него, сколько пришло гостей. Вася ответил: «Больше шести», а стоявшая рядом сестренка сказала: «Больше пяти».
Сколько было гостей, если известно, что один ответ верный, а другой нет?
Ответ. 6.
Решение. Допустим, что гостей действительно больше шести. Тогда правы и Вася, и его сестра, а это противоречит условию задачи. Значит, гостей не больше шести и Вася
неправ. Но тогда должна быть права сестра, иначе снова нарушится условие задачи. Значит, гостей больше пяти. Но если их больше пяти и не больше шести, то их ровно шесть.
7.2. В ящике 25 кг гвоздей. Как с помощью чашечных весов и одной гири в 1 кг за два взвешивания отмерить 19 кг гвоздей?
Решение. При первом взвешивании на одну из чашек весов кладем гирю и все гвозди раскладываем по чашкам так, чтобы установилось равновесие. Получим 13 и 12 кг гвоздей.
Первую кучку откладываем, а остальные гвозди делим пополам, взвешивая без гири: 12 = 6 + 6. Получили искомое количество гвоздей: 19 = 13 + 6
7.3. У Пети есть четыре орешка. Он всеми возможными способами брал по три орешка и взвешивал их на весах. Получилось 9 г, 14 г, 16 г и 18 г. Сколько весил каждый орешек?
Требуется найти все решения задачи и доказать, что других нет.
Ответ. 1, 3, 5, 10.
Решение. В сумме 9 + 14 + 16 + 18 = 57 вес каждого орешка сосчитан трижды, значит, суммарный вес всех орешков равен 19 г. Разность 19 – 9 = 10 – это вес одного из орешков.
Аналогично находим веса остальных орешков.
7.4. Квадрат состоит из одного внутреннего квадрата (чёрного) и четырех равных белых прямоугольников (см. рис. 2). Периметр каждого прямоугольника равен 40 см.Найдите
площадь чёрного квадрата.
Рис. 2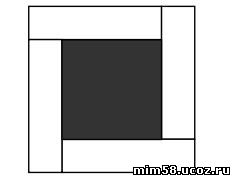
Ответ. 400.
Решение. Сумма длин короткой и длинной сторон прямоугольника равна 20. Но эта сумма равна стороне исходного квадрата.
7.5. Можно ли выложить в ряд 30 шариков – белых, синих и красных – так, чтобы среди любых двух идущих подряд шариков был хотя бы один белый, среди любых трёх идущих
подряд – хотя бы один синий, а среди любых пяти идущих подряд – хотя бы один красный?
Ответ объясните.
Ответ. Нельзя.
Первое решение. Допустим, можно. Возьмём красный шарик, не лежащий с краю (такой найдётся хотя бы в пятёрке шариков со 2-го по 6-ой). Соседние с ним шарики должны
быть белыми, иначе найдутся два соседних шарика, среди которых нет белых. Но это значит, что мы нашли три подряд идущих шарика, среди которых нет синего.
Второе решение. Разбив 30 шариков на 15 пар соседних шариков, убеждаемся, что среди выложенных шариков не меньше 15 белых. Разбив их на 10 троек подряд идущих
шариков, убеждаемся, что среди выложенных шариков не меньше 10 синих. Наконец, разбив их же на 6 пятёрок подряд идущих шариков, видим, что среди выложенных шариков не
меньше 6 красных. Получается, что шариков должно быть не меньше, чем 15 + 10 + 6 = 31, а их только 30.
Восьмой класс
_8_klass_2014.docРешение школьного тура олимпиады 8 класс
8.1. У Васи в кошельке лежало немного денег. Вася положил в кошелек еще 49 рублей, и сумма денег в кошельке увеличилась в 99 раз. Сколь денег стало у Васи в кошельке?
Ответ. 49 рублей 50 копеек.
Решение. Пусть вначале у Васи было x рублей. Из условия задачи получаем, что x + 49 = 99x. Решая это уравнение, получаем x = 0,5 рубля = 50 копеек.
8.2. Имеется 30 бревен длинами 3 и 4 м, суммарная длина которых равна 100 м. Каким числом распилов можно распилить бревна на чурбаны длиной 1 м? (Каждым распилом
пилится ровно одно бревно.)
Ответ. 70.
Первое решение. Склеим все бревна в одно 100-метровое бревно. Чтобы его разделить на 100 частей, нужно сделать 99 распилов, из которых 29 уже было
сделано.
Второе решение. Если было m трехметровых и n четырехметровых бревен, то m + n = 30, 3m + 4n = 100, откуда m = 20, n = 10. Поэтому нужно сделать 202 + 103 = 70
распилов.
8.3. Число a таково, что прямые y = ax + 1, y = x + a и y = 3 различны и пересекаются в одной точке. Каким может быть a?
Ответ. a = 2.
Первое решение. Заметим, что при x = 1 выполняется ax + 1 = x + a = a + 1, так что точка M (1; a + 1) является общей для прямых y = ax + 1 и y = x + a. Так как прямые
различны, M – их единственная общая точка. Поэтому прямая y = 3 тоже должна проходить через неё, откуда a + 1 = 3 и a = 2. Легко видеть, что при a = 2 все три прямые действительно
различны.
Второе решение. По условию в точке пересечения a x + 1 = x + a (a – 1)( x – 1) = 0,откуда a = 1 или x = 1. Но случай a = 1 невозможен, потому что тогда первые две прямые
совпадали бы. Дальше рассуждаем как в первом решении.



