Источники: А.Г. Ильяхов. Античные корни русского языка. Этимологический словарь.

Зачем нужны уравнения?

Вычислительные задачи бывают прямые и косвенные.

Вот пример прямой задачи: какова масса куска сплава, на изготовление которого пошло 0,6 дм³ меди (плотность 8,9 кг/дм³) и 0,4 дм³ цинка (плотность 7,0 кг/дм³)?

При ее решении находим массу взятой меди (8,9 · 0,6 = 5,34 кг), затем массу цинка (7,0 · 0,4 = 2,8 кг) и, наконец, массу сплава (5,34 + 2,8 = 8,14 кг). Выполняемые действия и их последовательность диктуются самим условием задачи.

Вот пример косвенной задачи: кусок сплава меди и цинка объемом в 1 дм³ имеет массу 8,14 кг. Найти объемные количества меди и цинка в этом сплаве. Здесь из условия задачи не видно, какие действия ведут к ее решению. При так называемом арифметическом решении нужно проявить подчас большую изобретательность, чтобы наметить план решения косвенной задачи. Каждая новая задача требует создания нового плана. Труд вычислителя затрачивается нерационально. Для рационализации вычислительного процесса и был создан метод уравнений, который является основным предметом изучения в алгебре. Суть этого метода такова.

1. Искомые величины получают особые обозначения. Мы пользуемся для этой цели буквенными знаками (предпочтительно последними строчными буквами латинского алфавита x, y, z, u, v).Условие задачи с помощью этих знаков и знаков действий (+, - и т. д.) «переводится на математический язык», т. е. связи между данными и искомыми величинами мы выражаем не словами и фразами разговорного языка, а математическими знаками. Каждая такая «математическая фраза» и есть уравнение.
2. После этого мы решаем уравнение, т. е. находим значения искомых неизвестных величин. Решение уравнения производится совершенно механически, по общим правилам. Нам не приходится больше учитывать особенности данной задачи; мы только должны применять раз навсегда установленные правила и приемы. (Выводом этих правил и занимается в первую очередь алгебра.)

Таким образом, уравнения нужны для того, чтобы механизировать труд вычислителя. После того как уравнение составлено, решение его можно получить вполне автоматически. Вся трудность решения задачи сводится лишь к составлению уравнения.

Источник: М. Я. Выгодский. Справочник по элементарной математике. Москва 1986.

                                                                                                       Цитаты и афоризмы (математики о математике)

***
Математика — это язык, на котором написана книга природы.
В конце концов, окружность бесконечно большого круга и прямая линия - одно и то же.Г. Галилей
***
Нельзя быть математиком, не будучи в то же время и поэтом в душе. С. Ковалевская
***
Нельзя быть настоящим математиком, не будучи немного поэтом.К.Вейерштрасс
***
Если теорему так и не смогли доказать, она становится аксиомой.Евклид
***
Всякий знает, что такое кривая, пока не выучится математике настолько, что вконец запутается в бесконечных исключениях.Ф. Клейн
***
Мнимые числа - это прекрасное и чудесное убежище божественного духа, почти что сочетание бытия с небытием. Г. В. Лейбниц
***
Математическая истина, независимо от того, в Париже или в Тулузе, одна и та же. Б. Паскаль
***
В математике нет символов для неясных мыслей.
Если кто-либо хочет кратким и выразительным словом определить само существо математики, тот должен сказать, что это наука о бесконечности. А. Пуанкаре
***
Математика является учением об отношениях между формулами, лишенными какого бы то ни было содержания Д. Гильберт
***
Геометрия - это искусство хорошо рассуждать на плохо выполненных чертежах. Н. Г. Абель
***
Науки математические с самой глубокой древности обращали на себя особенное внимание, в настоящее время они получили еще больше интереса по влиянию своему на искусство и промышленность.
П.Л. Чебышев
***
Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств. Л. Эйлер
***
Величие человека - в его способности мыслить. Б. Паскаль

О развитии практической геометрии в древней Руси.

 Уже в XVI в. нужды землемерия, строительства и военного дела при­вели к созданию рукописных руко­водств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как земля верстать». Оно является частью «Книги сошного пись­ма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г.

При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и "других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сво­дятся к определенным приемам решения задач на нахождение расстояний. Вот один пример.

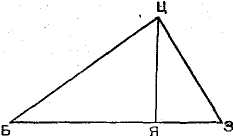
Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка 3 пересечения дру­гого катета (или его продолжения) с землей. Тогда расстоя­ние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей.